热传导问题的数值解法
本文参考杨世铭、陶文铨所著《传热学》第四版第四章。传热问题基本思想是将原来在时间、空间坐标系中连续的物理量场，用有限个离散点上的值的集合来代替，通过求解按一定方法建立起来的关于这些值的代数方程，来获得离散点上被求物理量的值。这些离散点上被求物理量值集合称为该物理量的数值解。
导热问题数值求解的基本思想
导热问题数值求解基本步骤
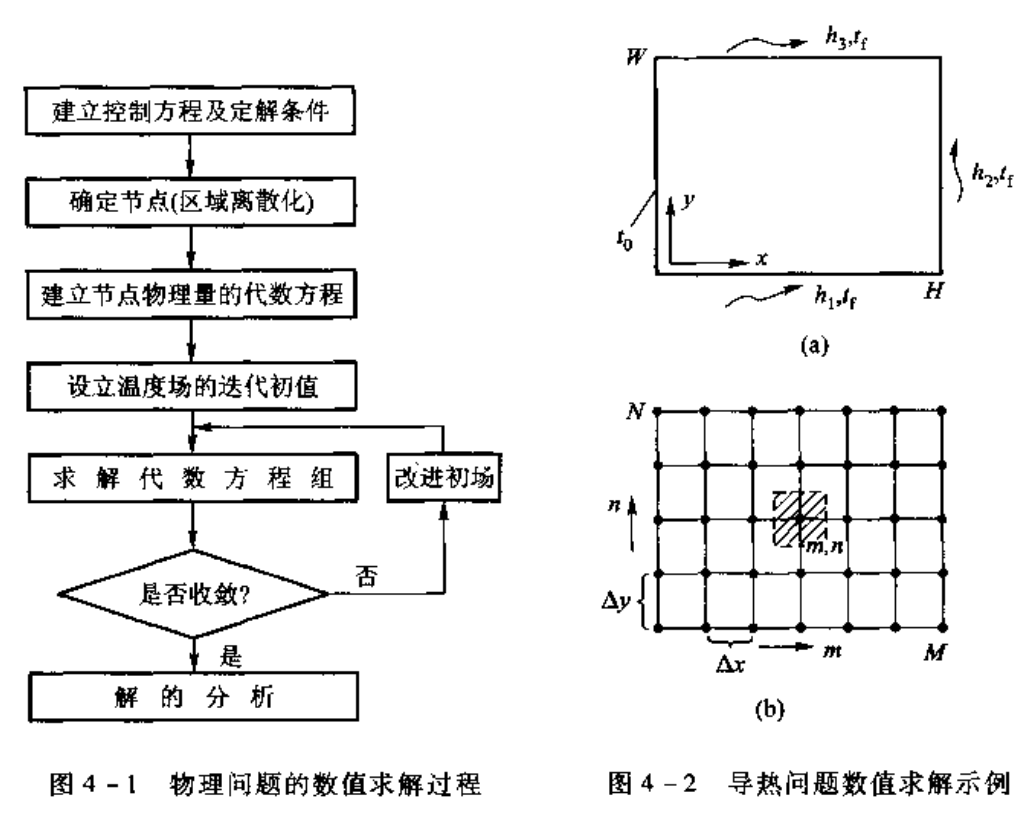
右上图所示的二维矩形域内稳态、无内热源、常物性的导热问题为例
- 建立控制方程及定解条件
导热微分方程 \[ \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} = 0. \]
四个边界条件分别为第一类和第三类边界条件。
- 区域离散化
将求解区域划分成许多子区域，以网格线的交点作为需要确定温度值的空间位置，称为节/结点（node）。相邻两节点的距离称为步长，记为\(~\Delta x\)、\(\Delta y\)。节点所代表的区域称为元体（element），又叫控制容积（control volume）。
- 建立节点物理量的代数方程
节点上物理的求解代数方程称为离散方程（discretization equation），考虑节点\(~(m,n)~\)的代数方程，当\(~\Delta x = \Delta y~\)时，内部节点代数方程满足 \[ T_{m,n} = \frac{1}{4}(T_{m+1,n} + T_{m-1,n} + T_{m,n+1} + T_{m,n-1}).\label{dis-eq} \]
- 设立迭代初始场
代数方程组的求解方法有直接法与迭代法两大类，传热问题的有限差分法中主要采用迭代法。采用此法求解时需要假定初始解，称为初场（initial field），在求解过程这一温度场不断得到改进。
- 求解代数方程
除\(~m=1~\)的左边界上各节点的温度为已知外，其余\(~(M-1)\times N~\)个节点都需要建立起类似于式\(~\eqref{dis-eq}~\)的离散方程，一共\(~(M-1)\times N~\)个代数方程，构成封闭的代数方程组。实际工程问题中，代数方程的个数一般在\(~10^3\sim 10^6~\)的数量级。针对上述问题，代数方程一旦建立，各项系数在整个求解过程不再变化，称为线性问题。如果物性为温度的函数，则式\(~\eqref{dis-eq}~\)右端 4 个邻点温度的系数不再是常数，而是温度的函数，这些系数在迭代过程中不断更新，这种问题称为非线性问题。
- 解的分析
获得物体中温度分布不是最终目的，所得的温度场可能进一步应用于计算热流量或计算设备、零部件的热应力及热变形。
内节点离散方程的建立方法
建立节点离散方程的方法有泰勒级数展开法及热平衡法两种，现以下图进行详细介绍
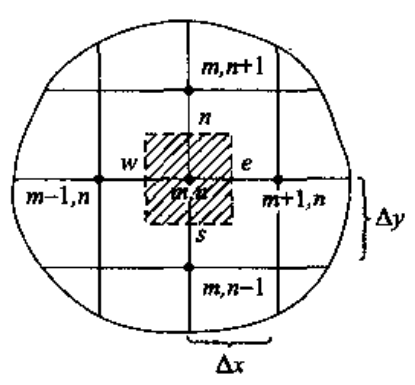
泰勒级数展开法
现以节点\(~(m,n)~\)处的二阶偏导数为例，导出其差分表达式，对节点\(~(m+1,n)~\)及\(~(m-1,n)~\)分别写出温度的泰勒级数展开式 \[ \begin{aligned} T_{m+1,n} = T_{m,n} + \Delta x \left. \frac{\partial T}{\partial x} \right |_{m.n} + \frac{\Delta x^2}{2} \left. \frac{\partial^2 T}{\partial x^2} \right |_{m.n} + \frac{\Delta x^3}{6} \left. \frac{\partial^3 T}{\partial x^3} \right |_{m.n} + \cdots,\\ T_{m-1,n} = T_{m,n} - \Delta x \left. \frac{\partial T}{\partial x} \right |_{m.n} + \frac{\Delta x^2}{2} \left. \frac{\partial^2 T}{\partial x^2} \right |_{m.n} - \frac{\Delta x^3}{6} \left. \frac{\partial^3 T}{\partial x^3} \right |_{m.n} + \cdots. \end{aligned} \] 以上两式相加得 \[ T_{m+1,n} + T_{m-1,n} = 2T_{m,n} + \Delta x^2 \left. \frac{\partial^2 T}{\partial x^2} \right |_{m.n} + \frac{\Delta x^4}{12} \left. \frac{\partial^4 T}{\partial x^4} \right |_{m.n}. \] 上式中重写为 \[ \left. \frac{\partial^2 T}{\partial x^2} \right|_{m,n} = \frac{T_{m+1,n} - 2 T_{m,n} + T_{m-1,n}}{\Delta x^2} + \mathcal{O}(\Delta x^2), \label{eq5} \] 其中\(~\mathcal{O}(\Delta x^2)~\)称为截断误差（truncation error），表示未明确写出得级数余项中\(~\Delta x~\)得最低阶数为 2。进行数值计算时，一般省略掉截断误差，此时差分表达式也被称为中心差分（central difference）。同理可得 \[ \left. \frac{\partial^2 T}{\partial y^2} \right|_{m,n} = \frac{T_{m,n+1} - 2 T_{m,n} + T_{m,n-1}}{\Delta y^2} + \mathcal{O}(\Delta y^2). \label{eq6} \] 将式\(~\eqref{eq5}~\)和\(~\eqref{eq6}~\)代入节点\(~(m,n)~\)得离散方程，忽略截断误差，则有 \[ \frac{T_{m+1,n} - 2 T_{m,n} + T_{m-1,n}}{\Delta x^2} + \frac{T_{m,n+1} - 2 T_{m,n} + T_{m,n-1}}{\Delta y^2} = 0. \label{eq7} \] 如果\(~\Delta x = \Delta y\)，则上式退回式\(~\eqref{dis-eq}\)。
下表列举了常见离散表达式
热平衡法
对每个节点代表的元体采用傅里叶定律，例如从节点\(~(m-1,n)~\)通过界面\(~w~\)传导到节点\(~(m,n)~\)的热流量可表示为 \[ \Phi_w = \lambda\Delta y\frac{T_{m-1,n}-T_{m,n}}{\Delta x}. \] 类似地，也可以写出通过其他三个界面\(~e\)、\(n~\)及\(~s~\)传导给节点\(~(m,n)~\)的热量，得到关于元体\(~(m,n)~\)的能量守恒方程 \[ \Phi_e + \Phi_w + \Phi_n + \Phi_s = 0, \] 即 \[ \begin{aligned} &\lambda\Delta y\frac{T_{m-1,n}-T_{m,n}}{\Delta x} + \lambda\Delta y\frac{T_{m+1,n}-T_{m,n}}{\Delta x} + \\ &\lambda\Delta x\frac{T_{m,n+1}-T_{m,n}}{\Delta y} + \lambda\Delta x\frac{T_{m,n-1}-T_{m,n}}{\Delta y} = 0. \end{aligned} \] 上式进一步简化可得到式\(~\eqref{eq7}\)。
边界节点离散方程的建立及代数方程的求解
边界节点离散方程的建立
对于第一类边界条件的导热问题，所有内节点的离散方程组成了一个封闭的代数方程组，可以立即进行求解。对于含有第二类或第三类边界条件的导热问题，由内节点的离散方程组成的方程组不封闭，因为包含了未知的边界温度，因此需要补充这类边界节点上的代数方程。这也是数值计算中边界处理问题。
在下面的讨论中，先把第二类边界条件及第三类边界条件合并起来考虑，并以\(~q_\text{w}~\)代表边界上已知的热流密度值或热流密度表达式（以热量进人计算区域为正），用热平衡方法导出三类典型边界节点的离散方程，然后针对\(~q_\text{w}~\)的一种不同情况使导得的离散方程进一步具体化。为使结果更具一般性，假设物体具有内热源\(~\dot{\Phi}\)（不必均布）。
- 位于平直边界上的节点
边界节点\(~(m,n)~\)代表半个元体，如下图所示。设边界上有向该元体传递的热流密度\(~q_\text{w}\)，于是该元体的能量守恒定律可表示为
\[
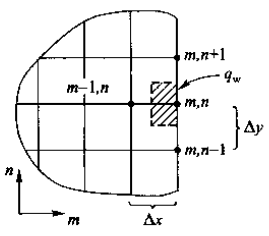\begin{aligned}
&\lambda \frac{T_{m-1,n}-T_{m,n}}{\Delta x}\Delta y +
\lambda \frac{T_{m,n+1}-T_{m,n}}{\Delta y}\frac{\Delta x}{2} + \\
&\lambda \frac{T_{m,n-1}-T_{m,n}}{\Delta y}\frac{\Delta x}{2} +
\frac{\Delta x \Delta y}{2}\dot{\Phi}_{m,n}+\Delta y q_\text{w} = 0.
\end{aligned}
\] 当\(~\Delta x = \Delta
y~\)时有 \[
T_{m,n} = \frac{1}{4}\left(2T_{m-1,n}+T_{m+1,n}+T_{m,n-1}+\frac{\Delta
x^2}{\lambda}\dot{\Phi}_{m,n}+\frac{2\Delta x}{\lambda}q_\text{w}
\right).
\]
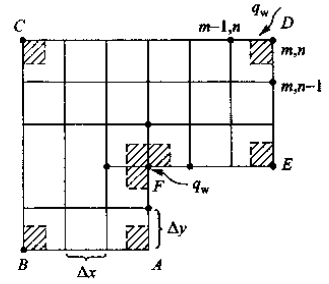
- 外部角点
在如下图所示的二维墙角计算区域中，节点 A ~ E 均为外部角点，其特点是每个节点仅代表四分之一个以\(~\Delta x\)、\(\Delta y~\)为边长的元体。今以外部角点 D 为例，假设其边界上有向该元体传递的热流密度\(~q_\text{w}\)，则其热平衡式为
\[
\begin{aligned}
&\lambda \frac{T_{m-1,n}-T_{m,n}}{\Delta x}\frac{\Delta y}{2} +
\lambda \frac{T_{m,n-1}-T_{m,n}}{\Delta y}\frac{\Delta x}{2} + \\
&
\frac{\Delta x \Delta y}{4}\dot{\Phi}_{m,n}+\frac{\Delta x+\Delta y}{2}
q_\text{w} = 0.
\end{aligned}
\] 当\(~\Delta x = \Delta
y~\)时有 \[
T_{m,n} = \frac{1}{2}\left(T_{m-1,n}+T_{m,n-1}+\frac{\Delta
x^2}{2\lambda}\dot{\Phi}_{m,n}+\frac{2\Delta x}{\lambda}q_\text{w}
\right).
\]
- 内部角点
如上图的 F 为内部角点，代表四分之三个元体。在同样的假设条件下有 \[ \begin{aligned} &\lambda \frac{T_{m-1,n}-T_{m,n}}{\Delta x}\Delta y + \lambda \frac{T_{m,n+1}-T_{m,n}}{\Delta y}\Delta x + \lambda \frac{T_{m,n-1}-T_{m,n}}{\Delta y}\frac{\Delta x}{2}+ \\ &\lambda \frac{T_{m+1,n}-T_{m,n}}{\Delta x}\frac{\Delta y}{2}+\frac{3\Delta x \Delta y}{4}\dot{\Phi}_{m,n}+\frac{\Delta x+\Delta y}{2} q_\text{w} = 0. \end{aligned} \] 当\(~\Delta x = \Delta y~\)时有 \[ T_{m,n} = \frac{1}{6}\left(2T_{m-1,n}+2T_{m,n+1}+T_{m,n-1}+T_{m+1,n}+\frac{3\Delta x^2}{2\lambda}\dot{\Phi}_{m,n}+\frac{2\Delta x}{\lambda}q_\text{w} \right). \] 边界热流密度的三种情况
- 绝热边界
令\(~q_\text{w}=0~\)即可。
- \(q_\text{w}~\)值不为零
以给定\(~q_\text{w}~\)值代入上述方程，但要注意上述三式中以传入计算区域的热量为正。
- 对流边界
此时\(~q_\text{w}=h(T_\text{f}-T_{m,n})\)，将此式代入上式中。
处理不规则区域的阶梯型逼近法
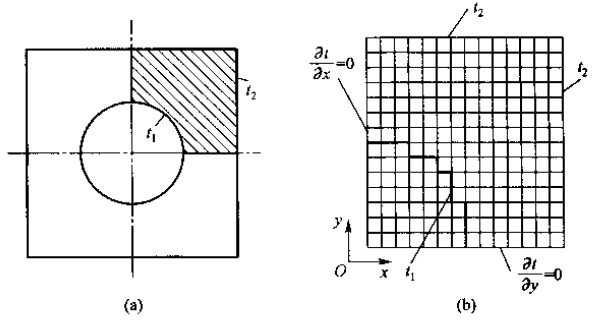
当计算区域中出现曲线边界或倾斜的边界时，常常用阶梯型的折线来模拟真实边界，然后再用上述方法建立起边界节点的离散方程。例如，要用数值方法确定如下左图所示二维区域的形状因子。显然，根据对称性只要考虑四分之一的计算区域即可。下左图中的内圆边界可以采用下右图所示的阶梯形的折线边界来近似。只要网格取得足够密,这种近似处理方法仍能获得相当准确的结果。
求解代数方程的迭代法
前已指出，代数方程组的求解方法分为直接解法及迭代法两大类。直接解法（direct method）是指通过有限次运算获得代数方程精确解的方法，像矩阵求 逆、高斯消元法等均属于此种方法。这一方法的缺点是计算所需的计算机内存 较大，当代数方程的数月较多时使用不便。另一类方法称迭代法（iteration method）。在迭代法中先对要计算的场作出假设（设定初场），在迭代计算过程中不断予以改进，直到计算前的假定值与计算后的结果相差小于允许值为止，称为迭代计算已经收敛。
- 高斯-赛德尔迭代法
- 迭代过程是否已经收敛的判据
迭代是否收敛的常用判据 \[ \max\left| T_i^{(k)}- T_i^{(k+1)} \right|\leq\varepsilon, \\ \max\left| \frac{T_i^{(k)}- T_i^{(k+1)}}{T_i^{(k)}} \right|\leq\varepsilon, \\ \max\left| \frac{T_i^{(k)}- T_i^{(k+1)}}{T_\text{max}^{(k)}} \right|\leq\varepsilon. \] 其中，上角标\(~k~\)及\(~(k+1)~\)表示迭代次数，\(T_\text{max}^{(k)}~\)为第\(~k~\)次迭代计算所得的计算区域中的最大值。一般允许的相对偏差为\(~\varepsilon=10^{-3}\sim10^{-6}\)。
- 迭代过程能否收敢的判据
迭代公式的选择应使每一个迭代变量的系数总是大于或等于该式中其他变量系数绝对值之和，此时用迭代法求解代数方程一定收敛。这一条件在数学上称为主对角线占优，简称对角占优（diagonal predominant）。