射流不稳定性
射流不稳定性即 Plateau–Rayleigh instability,也被称为 Rayleigh instability,用来解释射流断裂为液滴。射流不稳定性的驱动力为表面张力,其作用是使得液柱表面能最小。以下显示了水、甘油、聚乙二醇水溶液的断裂过程,该过程准确称法是下滴(Dripping),与射流(Jet)还是有所不同,前者流体速度慢,后者速度快。但两种过程分析方法相同。以下分析还是针对射流过程,分析过程来自于 MIT 课件。

重力下射流过程稳态分析
考虑流量为 \(Q\)、密度为 \(\rho\)、运动粘度为 \(\nu\) 的流体从一半径为 \(a\) 孔口向下流出,如下图所示。假设射流进口的雷诺数为 \(Re = Q/(a\nu)\) 足够大,可以忽略粘性。并且假设射流入口速度与半径无关。假设速度 \(U(z)\),液柱的半径为 \(r(z)\)。
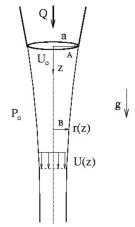
由伯努利定理知点 A 和 点 B 满足:
\[ \frac{1}{2}\rho U_0^2+\rho gz+P_\text{A}=\frac{1}{2}\rho U^2(z)+P_B. \]
局部曲率可以由两个主曲率 \(R_1\) 和 \(R_2\) 表示:
\[ \nabla\cdot\boldsymbol{n}=\frac{1}{R_1}+\frac{1}{R_2}\approx\frac{1}{r}. \] 点 A(入口)和点 B 的压力(Laplace 力)为:
\[ P_\text{A}\approx P_0+\frac{\sigma}{a},\quad P_\text{B}\approx P_0+\frac{\sigma}{r}. \]
综合可得:
\[ \frac{1}{2}\rho U_0^2+ \rho gz+P_0+\frac{\sigma}{a}=\frac{1}{2}\rho U^2(z)+P_0+\frac{\sigma}{r}, \]
解得:
\[ \frac{U(z)}{U_0}=\left[1+\frac{2}{\text{Fr}}\frac{z}{a}+\frac{2}{\text{We}}(1-\frac{a}{r})\right]^{1/2}, \]
其中
\[ Fr=\frac{U_0^2}{ga}=\frac{\text{Intertia}}{\text{Gravity}}=\text{Froude Number}, \]
\[ We=\frac{\rho U_0^2a}{\sigma}=\frac{\text{Intertia}}{\text{Curvature}}=\text{Weber Number}. \]
由流量守恒得:
\[ Q=2\pi \int_0^r U(z)r(z)\text{d}z=\pi a^2U_0=\pi r^2U(z), \]
因此
\[ \frac{r(z)}{a}=\left(\frac{U_0}{U(z)}\right)^{1/2}=\left[1+\frac{2}{\text{Fr}}\frac{z}{a}+\frac{2}{\text{We}}\left(1-\frac{a}{r}\right)\right]^{-1/4}, \]
当 \(We\rightarrow\infty\) 时,有:
\[ \frac{r(z)}{a}\left(1+\frac{2gz}{U_0^2}\right)^{-1/4},\quad\frac{U(z)}{U_0}=\left(1+\frac{2gz}{U_0^2}\right)^{1/2}. \]
扰动分析
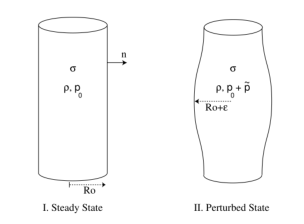
不考虑重力的话,平衡态包含无限长半径为 \(R_0\) 的流体柱。内部压力平衡边界处表面张力正应力
\[ p_0=\sigma \nabla\cdot\boldsymbol{n}\Rightarrow p_0=\frac{\sigma}{R_0}. \]
考虑小扰动,如上图所示。扰动表面假设如下,\(\epsilon\) 为扰动振幅(\(\epsilon\ll R_0\)):
\[ \widetilde{R}=R_0+\epsilon \mathrm{e}^{\omega t+\mathrm{i}kz}, \]
\(\omega\) 为不稳定增长率,可为复数,\(k\) 是轴向方向上的波数,相应的波长为 \(2\pi/k\)。
N-S 方程写作:
\[ \frac{\partial \boldsymbol{u}}{\partial t}+(\boldsymbol{u}\cdot\nabla)\boldsymbol{u}=-\frac{1}{\rho}\nabla p+\nu\Delta\boldsymbol{u}, \]
考虑无粘情况(\(\nu=0\)),假设 \(\widetilde{u}_r\) 为扰动速度得径向分量,\(\widetilde{u}_z\) 为轴向分量,\(\widetilde{p}\) 是扰动压力。将扰动量代入 N-S 方程得:
\[ \frac{\partial \widetilde{u}_r}{\partial t}=-\frac{1}{\rho}\frac{\partial \widetilde p}{\partial r},\quad\frac{\partial \widetilde{u}_z}{\partial t}=-\frac{1}{\rho}\frac{\partial \widetilde p}{\partial z}, \]
线性化连续性方程:
\[ \frac{\partial \widetilde{u}_r}{\partial r}+\frac{\widetilde{u}_r}{r}+\widetilde{u}_z=0. \]
假设速度、压力与表面有相同的形状的扰动:
\[ \widetilde{u}_r=R(r)\mathrm{e}^{\omega t+\mathrm{i} kz},\quad\widetilde{u}_z=Z(r)\mathrm{e}^{\omega t+\mathrm{i} kz},\quad\widetilde{p}=P(r)\mathrm{e}^{\omega t+\mathrm{i} kz}, \]
将上式代入线性化方程得动量方程
\[ \omega R=-\frac{1}{\rho} \frac{\mathrm{d}P}{\mathrm{d} r},\quad \omega Z=-\frac{\mathrm{i}k}{\rho}P, \]
和连续性方程
\[ \frac{\mathrm{d} R}{\mathrm{d} r}+\frac{R}{r}+\mathrm{i}kZ=0. \]
消除 \(Z(r)\) 和 \(P(r)\) 得到关于 \(R(r)\) 的方程:
\[ \boxed{r^2\frac{\mathrm{d}^2R}{\mathrm{d}r^2}+r\frac{\mathrm{d}R}{\mathrm{d}r}-(1+(kr)^2)R=0.} \] 令 \(r=kr\) 该方程做变换可得 \[ r^2\frac{\mathrm{d}^2 R}{\mathrm{d}r^2}+r\frac{\mathrm{d}R}{\mathrm{d}r}-(1+r^2)R=0. \]