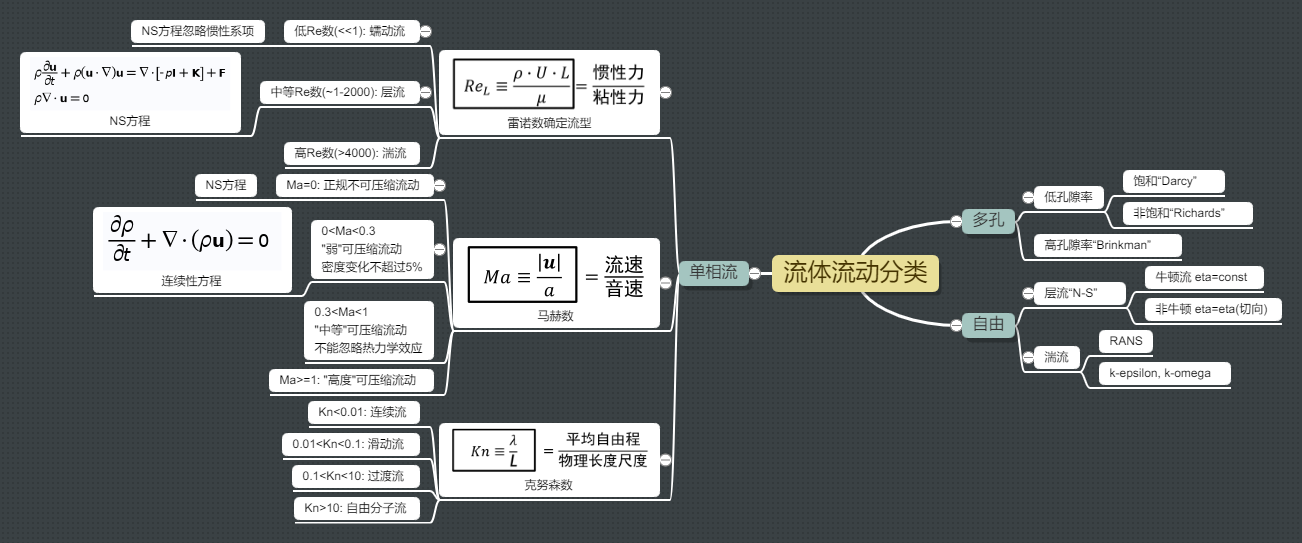
NS 方程索引
流体流动类型众多,可以按照流体粘性种类划分,也可以按照流体压缩性划分。本文参考了 COMSOL 帮助文档,列出主要常用的各种流体流动方程,以作参考。
标准 NS 方程
NS 方程用于描述速度场 \(\boldsymbol{u}\) 和压力场 \(p\) 的关系,可以写作 \[ \begin{align} \underbrace{\rho \left( \frac{\partial \boldsymbol{u}}{\partial t} + (\boldsymbol{u}\cdot\nabla) \boldsymbol{u} \right)}_\text{惯性力} & = \underbrace{-\nabla p}_\text{压力} + \underbrace{\nabla\cdot \boldsymbol{K}}_\text{粘性力} + \underbrace{\boldsymbol{F}}_\text{体积力}, \label{eq_momentum} \\ \frac{\partial \rho}{\partial t} + \nabla\cdot(\rho\boldsymbol{u}) & = 0. \label{eq_mass} \end{align} \] 其中 \(\rho\) 是流体密度,粘性力项中张量 \(\boldsymbol{K}\) 与动力粘度 \(\mu\) 和速度 \(\boldsymbol{u}\) 相关 \[ \boldsymbol{K} = \mu(\nabla \boldsymbol{u}+(\nabla\boldsymbol{u})^\mathsf{T})-\frac{2}{3}\mu((\nabla \cdot\boldsymbol{u})\boldsymbol{I}). \] 其中 \(\boldsymbol{I}\) 是单位矩阵,\(\nabla\boldsymbol{u}+(\nabla\boldsymbol{u})^\mathsf{T}=\boldsymbol{D}\) 也被称为变形率张量。如果流体不可压,则有 \(\text{d}\rho/\text{d}t=0\),代入方程 \(\eqref{eq_mass}\) 得 \(\nabla\cdot\boldsymbol{u}=0\)。假设流体粘度恒定,此时粘性力项可简化为 \[ \begin{align*} \nabla\cdot \boldsymbol{K} & = \nabla\cdot \left[ \mu(\nabla \boldsymbol{u}+(\nabla\boldsymbol{u})^\mathsf{T})-\frac{2}{3}\mu((\nabla \cdot\boldsymbol{u})\boldsymbol{I})\right] \\ & = \nabla \cdot \left[ \mu(\nabla \boldsymbol{u}+(\nabla\boldsymbol{u})^\mathsf{T})\right] \\ & = \mu \nabla \cdot \nabla \boldsymbol{u} = \mu \nabla^2\boldsymbol{u}. \end{align*} \] 则不可压、粘性、层流 NS 方程可写作 \[ \begin{equation}\label{eq_ns} \boxed{\begin{aligned} \rho \left( \frac{\partial \boldsymbol{u}}{\partial t} + (\boldsymbol{u}\cdot\nabla) \boldsymbol{u} \right) & = -\nabla p + \mu \nabla^2\boldsymbol{u} + \boldsymbol{F}, \\ \nabla\cdot\boldsymbol{u} & = 0. \end{aligned}} \end{equation} \] 流体的可压缩性可以通过无量纲数——马赫数 \[ Ma = U/c \] 来判定,其中 \(U\) 是流体特征速度, \(c\) 是流体声速。按马赫数大小可分为
- 不可压流动(\(Ma=0\))
- 弱可压缩流动(\(Ma<0.3\))
- 亚声速流动(\(Ma=0.3~0.8\) 左右)
- 跨声速流动(\(Ma=0.8~1.2\) 左右)
- 超声速流动(\(Ma=1.2~5.0\) 左右)
- 高超声速流动(\(Ma>5.0\))
不可压流动可通过方程 \(\eqref{eq_ns}\) 求解,弱可压缩流动可通过方程 \(\eqref{eq_momentum}\) 和 \(\eqref{eq_mass}\) 求解。当 \(Ma>0.3\) 需要考虑湍流效应和热效应,需要额外方程来描述流体流动特征。
对于不可压流动,描述湍流效应还有一重要的无量纲数——雷诺数 \[ Re=\frac{\rho UL}{\mu}=\frac{\text{惯性力}}{\text{粘性力}}, \] 其中 \(L\) 是流动结构特征长度。尽管不同的流动结构产生湍流效应的临界雷诺数不同,一般可认为当 \(Re>2000\) 时产生湍流效应,当 \(Re<2000\) 流体流动可通过方程 \(\eqref{eq_ns}\) 求解。如果惯性力相对于粘性力可以忽略(一般 \(Re<<1\)),流体流动及其缓慢,该种流动也被称为为蠕动流。在求解时,方程 \(\eqref{eq_ns}\) 中惯性项中对流项 \((\boldsymbol{u}\cdot\nabla) \boldsymbol{u}\) 可以忽略 \[ \begin{equation} \boxed{\begin{aligned} \rho \frac{\partial \boldsymbol{u}}{\partial t} & = -\nabla p + \mu \nabla^2\boldsymbol{u} + \boldsymbol{F}, \\ \nabla\cdot\boldsymbol{u} & = 0. \end{aligned}} \end{equation} \]
湍流
热效应
两相流
在工程上,有时需要追踪流体的界面,此时,表面张力在界面变形中起到重要作用。如最常见的水龙头接水时,液柱界面形状变化。考虑最普通的气液两相不可压流动,如下图所示
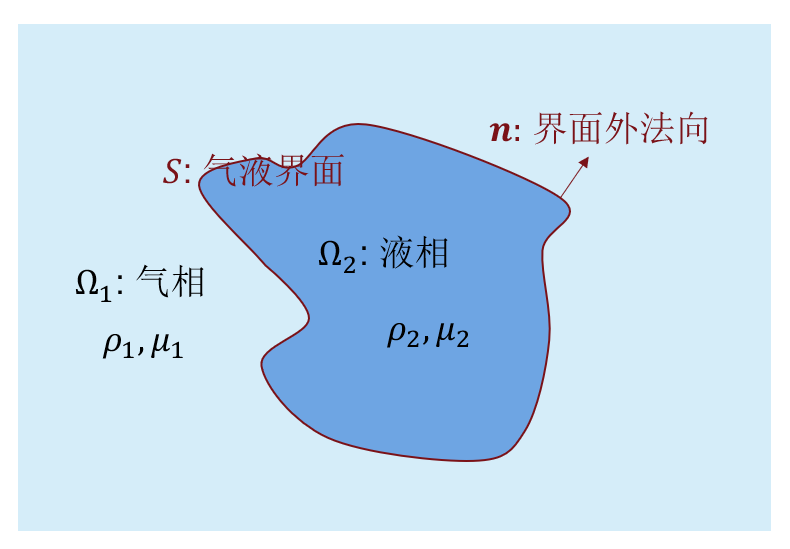
若空间内气液界面 \(\boldsymbol{s}=\boldsymbol{s}(\boldsymbol{\xi};t)\) 用两个参数 \(\boldsymbol{\xi}=(\xi_1,\xi_2)\) 的参数方程表示,则界面的运动方程满足 \[ \left( \frac{\partial \boldsymbol{s}(\boldsymbol{\xi};t)}{\partial t}-\boldsymbol{u}(\boldsymbol{\xi};t) \right)\cdot\boldsymbol{n} = 0, \] 其中 \(\boldsymbol{u}(\boldsymbol{\xi};t)\) 表示位置 \(\boldsymbol{\xi}=(\xi_1,\xi_2)\) 的速度,该方程通常也简写为动力学边界条件 \(\boldsymbol{n}\cdot(\boldsymbol{u}-\boldsymbol{u}_S)=0\),\(\boldsymbol{u}_S\) 是气液界面运动速度。如果用等值面 \(S(\boldsymbol{s}(\boldsymbol{\xi};t);t) = S_0\) 来表示气液界面,上式可写作 \[ \begin{align}\label{eq_S} \frac{\partial S}{\partial t} + \boldsymbol{u}\cdot \nabla S = 0. \end{align} \] 在气相和液相 \(\Omega_1\cup\Omega_2\) 中,流体流动均满足方程 \(\eqref{eq_ns}\) 。在气液界面 \(S\) 上,两侧的应力差驱动界面流动,满足界面应力平衡方程 \[ \begin{align}\label{bc_stress} \boxed{\boldsymbol{n}\cdot[\boldsymbol{T}_i]_2^1=\gamma\kappa\boldsymbol{n},} \end{align} \] 其中 \([x_i]_2^1=x_1-x_2\) 表示物理量跨越界面时的差值,\(\boldsymbol{T}_i=-p_i\boldsymbol{I} \boldsymbol+\mu_i\boldsymbol{D}_i\) 称为水动力应力张量(hydrodynamic stress tensor),\(\kappa=-\nabla\cdot \boldsymbol{n}\) 是界面平均曲率。如果气液两相可当作无粘流体或者均处于静止状态,则两侧压力差为 \[ \Delta p=p_1-p_2=\gamma\kappa, \] 该压力差也被称为拉普拉斯压力。注意NS 方程是体方程,而方程 \(\eqref{bc_stress}\) 是表面方程。追踪界面方法有流体体积(Volume of fluid, VOF)法、水平集(Level set,LS)法和任意拉格朗日(Arbitrary Lagrangian Eulerian,ALE)法等。其中 VOF 和 LS 法将界面处理成一定厚度的过渡层。
VOF 方法
VOF 法引入相体积分数 \(c\) 来实现对计算域内界面进行追踪,同时将双流体方程(气液相各一个)转化为单流体方程。流体体积分数一般设置为 \[ \left\{ \begin{align*} & c=0 & \text{气相} \\ & 0<c<1 & \text{界面} \\ & c = 1 & \text{液相} \end{align*}. \right. \]
通过求出整个计算域内各网格单元的相分数,从而可以构建出界面
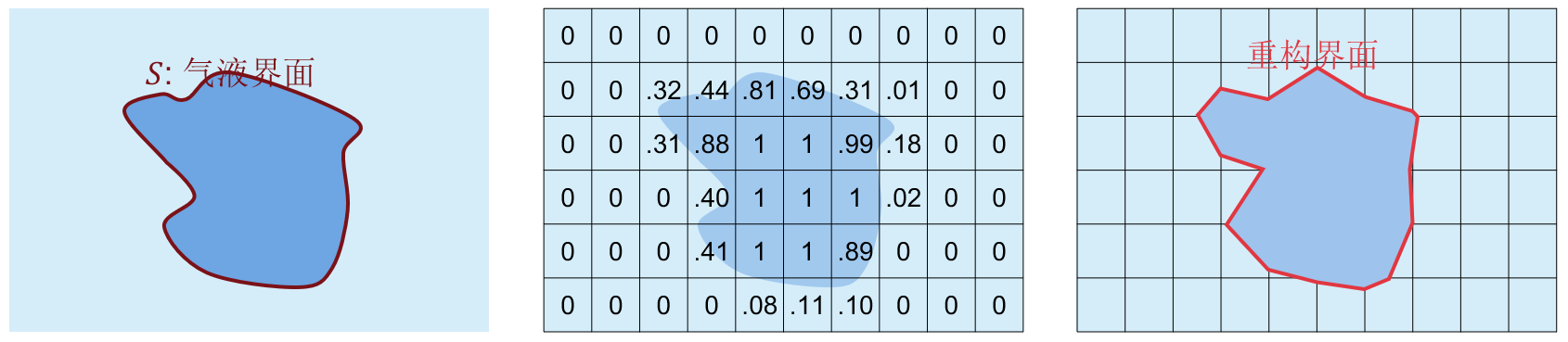
在 VOF 法中,所有物理量经过界面都是渐变的,如转化为单流体方程中密度和粘度可表示为 \[ \rho(c)=(1-c)\rho_1+c\rho_2,\ \mu(c)=(1-c)\mu_1+c\mu_2. \] 此时求解的单流体动量方程为 \[ \begin{align} \rho(c) \left( \frac{\partial \boldsymbol{u}}{\partial t} + (\boldsymbol{u}\cdot\nabla) \boldsymbol{u} \right) = \nabla \cdot \boldsymbol{T} + \boldsymbol{F_S},\label{eq_mo} \end{align} \] 此处我们用 \(\boldsymbol{T} = -p\boldsymbol{I} \boldsymbol+\mu(c)\boldsymbol{D}\) 代替了 \(\eqref{eq_ns}\) 中的压力项和粘性项,\(\boldsymbol{F_S}\) 为表面张力导出的体积力。单流体仍然当作是不可压流体,有 \[ \frac{\text{d}\rho}{\text{d}t} = 0 \rightarrow \frac{\text{d} \left((1-c)\rho_1+c\rho_2 \right)}{\text{d}t}= (\rho_2-\rho_1)\frac{\text{d}c}{\text{d}t} = 0, \] 即 \[ \boxed{\frac{\partial c}{\partial t}+\boldsymbol{u}\cdot\nabla c=0.} \] 该方程是不可压缩 VOF 模型中的相方程,也是最常见的对流方程,也与方程 \(\eqref{eq_S}\) 一致。VOF 模型中,界面法向向量和曲率可以写为 \[ \boldsymbol{n}=\frac{\nabla c}{\left |\nabla c \right|},\ \kappa = -\nabla \cdot \left( \frac{\nabla c}{\left |\nabla c \right|} \right). \] 为了将表面方程 \(\eqref{bc_stress}\) 考虑到 VOF 方法中,需要用到连续力(Continuum surface force,CSF)模型,该模型将间断的压力处理成连续过渡的体积力,即(不考虑马兰戈尼效应) \[ \boldsymbol{n}\cdot(\boldsymbol{T}_1-\boldsymbol{T}_2)=\gamma\kappa\boldsymbol{n}\rightarrow \nabla \cdot \boldsymbol{T} = \nabla (\gamma\kappa)=\gamma\kappa\nabla c, \] 结合方程 \(\eqref{eq_mo}\) 不可压缩 VOF 模型中动量方程 \[ \boxed{\rho(c) \left( \frac{\partial \boldsymbol{u}}{\partial t} + (\boldsymbol{u}\cdot\nabla) \boldsymbol{u} \right) = -\nabla p + \nabla\cdot \left( \mu(c)\boldsymbol{D} \right) - \gamma \nabla \cdot \left( \frac{\nabla c}{\left |\nabla c \right|} \right) \nabla c.} \]