Gerris 入门教程

发表于 更新于 分类于

Gerris 是一款用于求解流体流动的软件包，能够准确描述两相流界面形变。其源码采用 C 语言编译，因此 Gerris 脚本可以内嵌标准的 C 语言函数。本文介绍如何写一个简单的 Gerris 脚本，原文请见此。注意，请确保你已经安装了 Gerris，安装教程可参考我的之前博客。由于 Gerris 在类 Unix 平台下运行，因此你需要熟悉类 Unix 的基本命令。

一个简单的脚本文件

Gerris 输入脚本由模拟域，网格划分与初始条件，边界条件，固体边界，输出内容和控制参数与数值算法几部分组成。注意，Gerris 中求解的是无量纲化NS 方程，所有物理量都是无量纲的，默认粘度、表面张力等量为 0。

以下以一个初始随机涡量的例子说明 Gerris 脚本。在命令窗口输入以下命令新建vorticity.gfs脚本：

1
2
3
mkdir vorticity
cd vorticity
vi vorticity.gfs

粘贴以下内容

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# 模拟区域
1 2 GfsSimulation GfsBox GfsGEdge {} {
# 模拟时间
  GfsTime { end = 50 }
# 网格划分
  GfsRefine 6
# 初始条件
  GfsInit {} {
    U = (0.5 - rand()/(double)RAND_MAX)
    V = (0.5 - rand()/(double)RAND_MAX)
  }
# 输出信息，打印在命令窗口
  GfsOutputTime            { istep = 10   } stdout
  GfsOutputProjectionStats { istep = 10   } stdout
  GfsOutputScalarStats     { istep = 10   } stdout { v = Vorticity }
# 输出信息，写入文件
  GfsOutputPPM             { step = 0.1 } { ppm2gif > vorticity.gif } {
    v = Vorticity 
    min = -10
    max =  10
  }
}
# 边界条件c
GfsBox {}
1 1 right
1 1 top

在命令窗口输入以下以进行运算：

1
gerris2D vorticity.gfs

运行完后会生成vorticity.gif文件，如下所示：

模拟域

vorticity.gfs第 1 行1 2 GfsSimulation GfsBox GfsGEdge {} {}由 7 个块组成，定义了模拟域的布局。

  • 第 1 个块：定义节点（node）数，如第 1 行中的1
  • 第 2 个块：定义连接节点的边（edge）数，如第 1 行中2
  • 第 3 个块：定义模拟对象类型，如第 1 行中GfsSimulation
  • 第 4 个块：定义节点的默认对象类型，如第 1 行中GfsBox
  • 第 5 个块：定义边的对象类型，如第 1 行中的GfsEdge
  • 第 6 个块：第 1 个可选参数，如第 1 行中的前一个大括号
  • 第 7 个块：第 2 个可选参数，如第 1 行中的后一个大括号

因此该行定义了一个模拟盒子（box），模拟盒子有 2 条边存在连接。

边界条件

模拟盒子有 2 条边存在连接情况由最后三行

1
2
3
GfsBox {}
1 1 right
1 1 top

定义。模拟盒子的右边（right）和上边（top）与自己相连，这相当于定义了周期性边界条件。Gerris 中盒子方向如下定义，默认情况下，二维为正方形，三维为正方体。GfsSimulation以1号盒子的中心为坐标原点，GfsAxi以1号盒子 bottom 边中心为坐标原点。

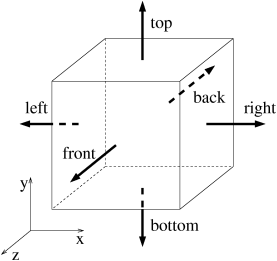
这个例子采用周期性边界条件，并没有指定如速度入口等边界条件。

网格划分与初始条件

vorticity.gfs第 3 行GfsRefine 6定义了网格划分，6表示网格细分级别，模拟盒子被划分为 \(2^6\times2^6\) 个网格。我们也可以采用GfsRefine 6.*(1. - sqrt (x*x + y*y))定义一个变细分级别的网格。

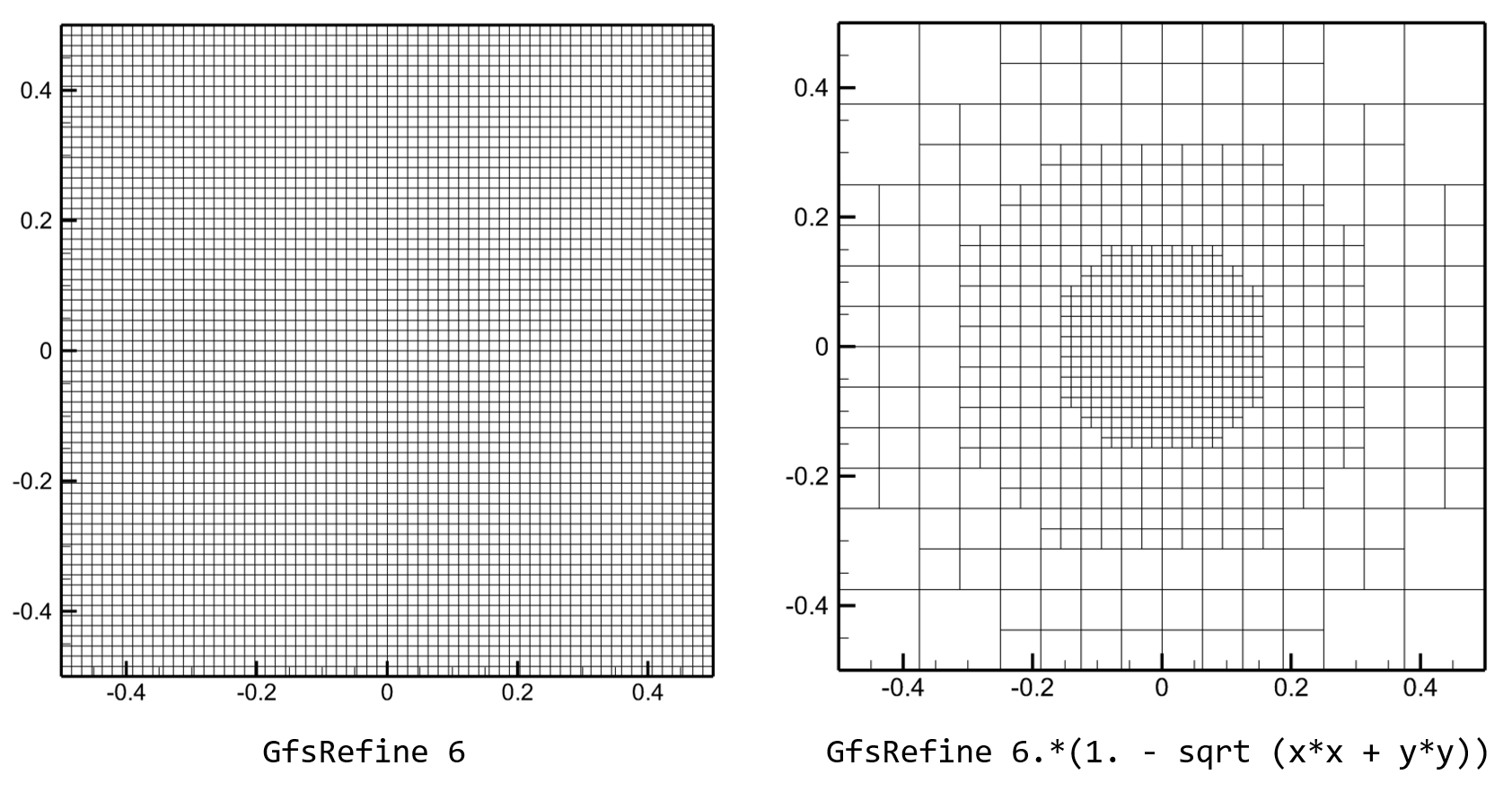
第 4-6 行

1
2
3
4
GfsInit {} {
  U = (0.5 - rand()/(double)RAND_MAX)
  V = (0.5 - rand()/(double)RAND_MAX)
}

定义初始速度条件，其它量如压力等默认情况下都为 0。rand()为 C 语言标准随机函数。

输出内容

vorticity.gfs第 8-15 行 均为输出内容，其中第 8-10 行为在命令窗口上打印内容，

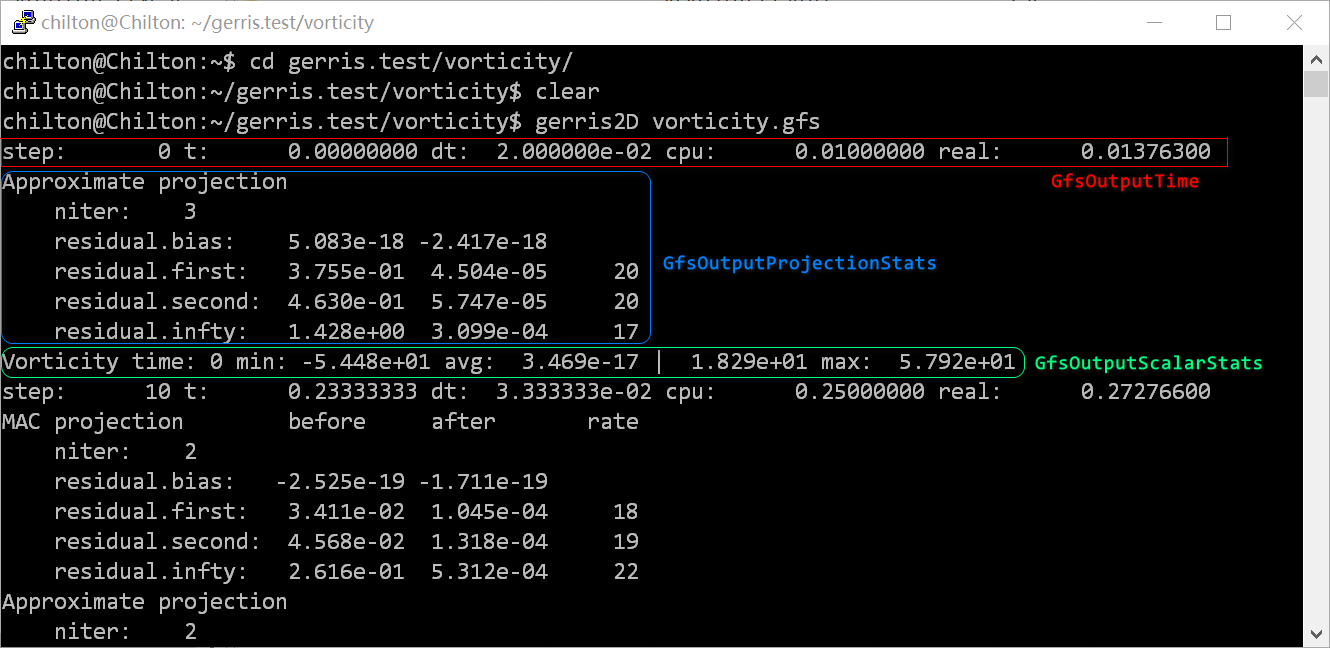
第 11-15 行为写入模拟结果到vorticity.gif，其中 PPM 为一种图像格式，可用 ACDSee 软件打开。考虑到后期处理，建议输出vtk格式或plt格式，具体可参考GfsOutputSimulation命令。

1
2
3
4
5
6
7
GfsOutputSimulation { step = 1 } name.vtk {
format = VTK
}
# 或者
GfsOutputSimulation { step = 1 } name.plt {
format = Tecplot
}