NS 方程中矢量计算

发表于 2020-01-22 更新于 2020-03-12 分类于研究相关

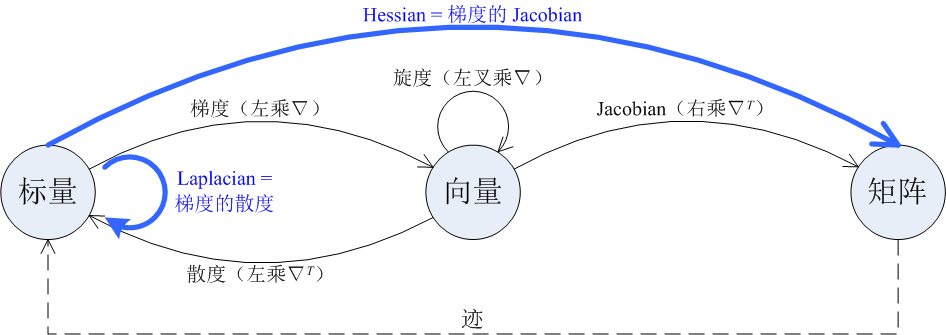
在 NS 方程中，常常会涉及标量，向量，张量。比如压力 \(p\) 为标量，速度 \(\boldsymbol{u}\) 为向量，剪切应力 \(\boldsymbol{\tau}\) 为张量。考虑三维体系，则标量为 \(1\times1\) 的 0 维矩阵，向量为 \(3\times1\) 的 1 维矩阵，二维张量为 \(3\times3\) 的 2 维矩阵。矢量运算涉及梯度运算和散度运算，还有旋度计算，下图展示了一些矢量之间关系。本文列举三种坐标系下 NS 方程中常见的矢量运算表达式，主要参考 Jens Eggers 书籍《Singularities Formation, Structure, and Propagation》中附录 A。

直角坐标系

设直角坐标系（Cartesian coordinates）下三个基向量分别为 \(\boldsymbol{e}_x=(1,0,0)\)，\(\boldsymbol{e}_y=(0,1,0)\)，\(\boldsymbol{e}_z=(0,0,1)\)，则该坐标系下的矢量可表示为

\[ \boldsymbol{u}=(u,v,w)=u\boldsymbol{e}_x+v\boldsymbol{e}_y+w\boldsymbol{e}_z. \]

设 \(\phi({\boldsymbol{r}})\) 为标量场，\(\boldsymbol{u}(\boldsymbol{r})\) 为向量场，其中 \(\boldsymbol{r}=(x,y,z)\) 为空间位置坐标。标准的 nabla 算子写作 \[ \nabla=\boldsymbol{e}_x \frac{\partial}{\partial x}+\boldsymbol{e}_y \frac{\partial}{\partial y}+\boldsymbol{e}_z \frac{\partial}{\partial z}. \]

则梯度（gradient）运算写作

\[ \text{grad}\ \phi=\nabla \phi=\frac{\partial \phi}{\partial x} \boldsymbol{e}_x+\frac{\partial \phi}{\partial y} \boldsymbol{e}_y+\frac{\partial \phi}{\partial z} \boldsymbol{e}_z, \]

类似于升维。散度（divergence）运算写作 \[ \text{div}\ \boldsymbol{u} = \nabla \cdot \boldsymbol{u}=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}, \]

类似于降维。旋度（curl）运算写作

\[ \text{curl} \ \boldsymbol{u} = \nabla \times \boldsymbol{u}=\left(\frac{\partial w}{\partial y}-\frac{\partial v}{\partial z}\right) \boldsymbol{e}_x+\left(\frac{\partial u}{\partial z}-\frac{\partial w}{\partial x}\right) \boldsymbol{e}_y+\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right) \boldsymbol{e}_z. \]

标量拉普拉斯（Laplacian）运算写作

\[ \Delta\phi=\nabla\cdot\nabla\phi=\frac{\partial^2 \phi}{\partial x^2}+\frac{\partial^2 \phi}{\partial y^2}+\frac{\partial^2 \phi}{\partial z^2}, \]

标量对流导数（convective derivative）写作

\[ (\boldsymbol{u}\cdot\nabla)\phi=u\frac{\partial\phi}{\partial x}+v\frac{\partial\phi}{\partial y}+w\frac{\partial\phi}{\partial z}. \] 矢量拉普拉斯（Laplacian）运算和对流导数（convective derivative）分别写作

\[ \begin{aligned} \Delta\boldsymbol{u} & =(\Delta u,\Delta v,\Delta w), \\ (\boldsymbol{u}\cdot\nabla)\boldsymbol{u} & =((\boldsymbol{u}\cdot\nabla)u, (\boldsymbol{u}\cdot\nabla)v,(\boldsymbol{u}\cdot\nabla)w). \end{aligned} \] 在 NS 方程中，经常会出现变形率张量 \(\boldsymbol{D}\)，可以写作 \[ \boldsymbol{D}=\nabla\boldsymbol{u}+(\nabla\boldsymbol{u})^\mathsf{T}, \]

其中 \[ \nabla \boldsymbol{u} = (\nabla u,\nabla v,\nabla w) = \left( \begin{matrix} \partial u /\partial x & \partial v /\partial x & \partial w /\partial x \\ \partial u /\partial y & \partial v /\partial y & \partial w /\partial y \\ \partial u /\partial z & \partial v /\partial z & \partial w /\partial z \end{matrix} \right). \]

柱坐标系

柱坐标系（Cylindrical coordinates） \(r\)，\(\theta\)，\(z\) 定义空间位置为 \(\boldsymbol{r}=(r\cos\theta,r\sin\theta,z)\)，则三个单位基向量分别为 \[ \boldsymbol{e}_r=(\cos\theta,\sin\theta,0),\boldsymbol{e}_\theta=(-\sin\theta,\cos\theta,0),\boldsymbol{e}_z=(0,0,1), \] 则该坐标系下的矢量可表示为 \[ \boldsymbol{u}=u_r\boldsymbol{e}_r+u_\theta\boldsymbol{e}_\theta+u_z\boldsymbol{e}_z. \] nabla 算子写作 \[ \nabla=\boldsymbol{e}_r \frac{\partial}{\partial r}+\frac{\boldsymbol{e}_\theta}{r} \frac{\partial}{\partial \theta}+\boldsymbol{e}_z \frac{\partial}{\partial z}, \]

则梯度，散度，旋度，标量拉普拉斯，矢量拉普拉斯运算和对流导数分别写作 \[ \nabla\phi=\frac{\partial\phi}{\partial r}\boldsymbol{e}_r+\frac{1}{r}\frac{\partial\phi}{\partial\theta}\boldsymbol{e}_\theta+\frac{\partial\phi}{\partial z}\boldsymbol{e}_z, \]

\[ \nabla\cdot\boldsymbol{u}=\frac{1}{r}\frac{\partial(r u_r)}{\partial r}+\frac{1}{r}\frac{\partial u_\theta}{\partial\theta}+\frac{\partial u_z}{\partial z}, \]

\[ \nabla\times\boldsymbol{u}= \frac{1}{r} \left|\begin{matrix} \boldsymbol{e}_r & r\boldsymbol{e}_\theta & \boldsymbol{e}_z \\ \partial/\partial r & \partial/\partial \theta & \partial/\partial z \\ u_r & r u_\theta & u_z \end{matrix}\right|, \]

\[ \Delta \phi=\frac{\partial^2\phi}{\partial r^2}+ \frac{1}{r}\frac{\partial\phi}{\partial r}+ \frac{1}{r^2}\frac{\partial^2\phi}{\partial \theta^2}+ \frac{\partial^2\phi}{\partial z^2}, \]

\[ \begin{aligned} (\boldsymbol{u}\cdot\nabla)\boldsymbol{u} & = \left( u_r\frac{\partial u_r}{\partial r}+\frac{u_\theta}{r}\frac{\partial u_r}{\partial \theta}+u_z\frac{\partial u_r}{\partial z}-\frac{u_\theta^2}{r} \right)\boldsymbol{e}_r \\ & + \left(u_r \frac{\partial u_\theta}{\partial r} + \frac{u_\theta}{r}\frac{\partial u_\theta}{\partial \theta} +u_z \frac{\partial u_\theta}{\partial z} + \frac{u_r u_\theta}{r} \right)\boldsymbol{e}_\theta \\ & + \left(u_r\frac{\partial u_z}{\partial r}+\frac{u_\theta}{r} \frac{\partial u_z}{\partial \theta} + u_z \frac{\partial u_z}{\partial z}\right)\boldsymbol{e}_z, \end{aligned} \]

\[ \Delta\boldsymbol{u}=\left( \Delta u_r-\frac{2}{r^2}\frac{\partial u_\theta}{\partial \theta}-\frac{u_r}{r^2} \right)\boldsymbol{e}_r+\left( \Delta u_\theta+\frac{2}{r^2}\frac{\partial u_r}{\partial \theta}-\frac{u_\theta}{r^2} \right)\boldsymbol{e}_\theta + \Delta u_z \boldsymbol{e}_z. \]

柱坐标系下的变形率张量的分量分别为 \[ \begin{aligned} & D_{rr}=2\frac{\partial u_r}{\partial r},\ D_{r\theta}=\frac{1}{r}\frac{\partial u_r}{\partial \theta}+\frac{\partial u_\theta}{\partial r}-\frac{u_\theta}{r}, \\ & D_{\theta\theta}=\frac{2}{r}\frac{\partial u_\theta}{\partial \theta}+\frac{2 u_r}{r},\ D_{\theta z}=\frac{\partial u_\theta}{\partial z}+\frac{1}{r}\frac{\partial u_z}{\partial \theta}, \\ & D_{zz}=2\frac{\partial u_z}{\partial z},\ D_{zr}=\frac{\partial u_z}{\partial r}+\frac{\partial u_r}{\partial z}. \end{aligned} \]

球坐标系

球坐标系（Spherical coordinates） \(r\)，\(\theta\)，\(\varphi\) 定义空间位置为 \(\boldsymbol{r}=(r\sin\theta\cos\varphi,r\sin\theta\sin\varphi,r\cos\theta)\)，则三个单位基向量分别为 \[ \begin{aligned} &\boldsymbol{e}_r=(\sin\theta\cos\varphi,\sin\theta\sin\varphi,\cos\theta), \\ &\boldsymbol{e}_\theta=(\cos\theta\cos\varphi,\cos\theta\sin\varphi,-\sin\theta), \\ &\boldsymbol{e}_\varphi=(-\sin\varphi,\cos\varphi,0); \end{aligned} \] 则该坐标系下的矢量可表示为 \[ \boldsymbol{u}=u_r\boldsymbol{e}_r+u_\theta\boldsymbol{e}_\theta+u_\varphi\boldsymbol{e}_\varphi. \] nabla 算子写作 \[ \nabla=\boldsymbol{e}_r \frac{\partial}{\partial r}+\frac{\boldsymbol{e}_\theta}{r} \frac{\partial}{\partial \theta}+\frac{\boldsymbol{e}_\varphi}{r\sin\theta} \frac{\partial}{\partial \varphi}, \]

\[ \nabla\cdot\boldsymbol{u}=\frac{1}{r^2}\frac{\partial(r^2u_r)}{\partial r}+\frac{1}{r\sin\theta}\frac{\partial (\sin\theta \ u_\theta)}{\partial\theta}+\frac{1}{r\sin\theta}\frac{\partial u_\varphi}{\partial \varphi}, \]

\[ \nabla\times\boldsymbol{u}= \frac{1}{r^2\sin\theta} \left|\begin{matrix} \boldsymbol{e}_r & r\boldsymbol{e}_\theta & r\sin\theta \ \boldsymbol{e}_\varphi \\ \partial/\partial r & \partial/\partial\theta & \partial/\partial\varphi \\ u_r & r u_\theta & r\sin\theta \ u_\varphi \end{matrix}\right|, \]

\[ \Delta \phi=\frac{1}{r^2}\frac{\partial}{\partial r} \left( r^2\frac{\partial \phi}{\partial r} \right)+ \frac{1}{r^2\sin\theta}\frac{\partial}{\partial \theta} \left( \sin\theta \frac{\partial \phi}{\partial \theta} \right)+ \frac{1}{r^2\sin^2\theta}\frac{\partial^2\phi}{\partial \varphi^2}, \]

\[ \begin{aligned} (\boldsymbol{u}\cdot\nabla)\boldsymbol{u} & = \left( u_r\frac{\partial u_r}{\partial r}+\frac{u_\theta}{r}\frac{\partial u_r}{\partial \theta}+\frac{u_\varphi}{r\sin\theta}\frac{\partial u_r}{\partial \varphi}-\frac{u_\theta^2+u_\varphi^2}{r} \right)\boldsymbol{e}_r \\ & + \left(u_r \frac{\partial u_\theta}{\partial r} + \frac{u_\theta}{r}\frac{\partial u_\theta}{\partial \theta} + \frac{u_\varphi}{r\sin\theta} \frac{\partial u_\theta}{\partial \varphi} + \frac{u_r u_\theta}{r} - \frac{u_\varphi^2\cot\theta}{r} \right)\boldsymbol{e}_\theta \\ & + \left(u_r\frac{\partial u_\varphi}{\partial r}+\frac{u_\theta}{r} \frac{\partial u_\varphi}{\partial \theta} + \frac{u_\varphi}{r\sin\theta} \frac{\partial u_\varphi}{\partial \varphi} + \frac{u_r u_\varphi}{r}+\frac{u_\theta u_\varphi \cot\theta}{r} \right)\boldsymbol{e}_\varphi, \end{aligned} \]

\[ \begin{aligned} \Delta\boldsymbol{u} & =\left( \Delta u_r-\frac{2 u_r}{r^2} - \frac{2}{r^2\sin\theta} \frac{\partial u_\theta\sin\theta}{\partial \theta}-\frac{2}{r^2\sin\theta}\frac{\partial u_\varphi}{\partial \varphi} \right)\boldsymbol{e}_r \\ & + \left( \Delta u_\theta+\frac{2}{r^2}\frac{\partial u_r}{\partial \theta}-\frac{u_\theta}{r^2\sin^2\theta} -\frac{2\cos\theta}{r^2\sin^2\theta} \frac{\partial u_\varphi}{\partial \varphi} \right)\boldsymbol{e}_\theta \\ & + \left( \Delta u_z + \frac{2}{r^2\sin\theta}\frac{\partial u_r}{\partial \varphi} + \frac{2\cos\theta}{r^2\sin^2\theta}\frac{\partial u_\theta}{\partial \varphi} - \frac{u_\varphi}{r^2 \sin^2\theta} \right) \boldsymbol{e}_\varphi. \end{aligned} \]

柱坐标系下的变形率张量的分量分别为 \[ \begin{aligned} & D_{rr}=2\frac{\partial u_r}{\partial r},\ D_{r\theta}=\frac{1}{r}\frac{\partial u_r}{\partial \theta}+\frac{\partial u_\theta}{\partial r}-\frac{u_\theta}{r}, \\ & D_{\theta\theta}=\frac{2}{r}\frac{\partial u_\theta}{\partial \theta}+\frac{2 u_r}{r},\ D_{\theta \varphi}=\frac{1}{r\sin\theta}\frac{\partial u_\theta}{\partial \varphi}+\frac{1}{r}\frac{\partial u_\varphi}{\partial \theta} - \frac{u_\varphi\cot\theta}{r}, \\ & D_{zz}=\frac{2}{r\sin\theta}\frac{\partial u_\varphi}{\partial \varphi} + \frac{2 u_r}{r} + \frac{2 u_\theta\cot\theta}{r},\ D_{\varphi r}=\frac{\partial u_\varphi}{\partial r} + \frac{1}{r\sin\theta}\frac{\partial u_r}{\partial \varphi} - \frac{u_\varphi}{r}. \end{aligned} \]